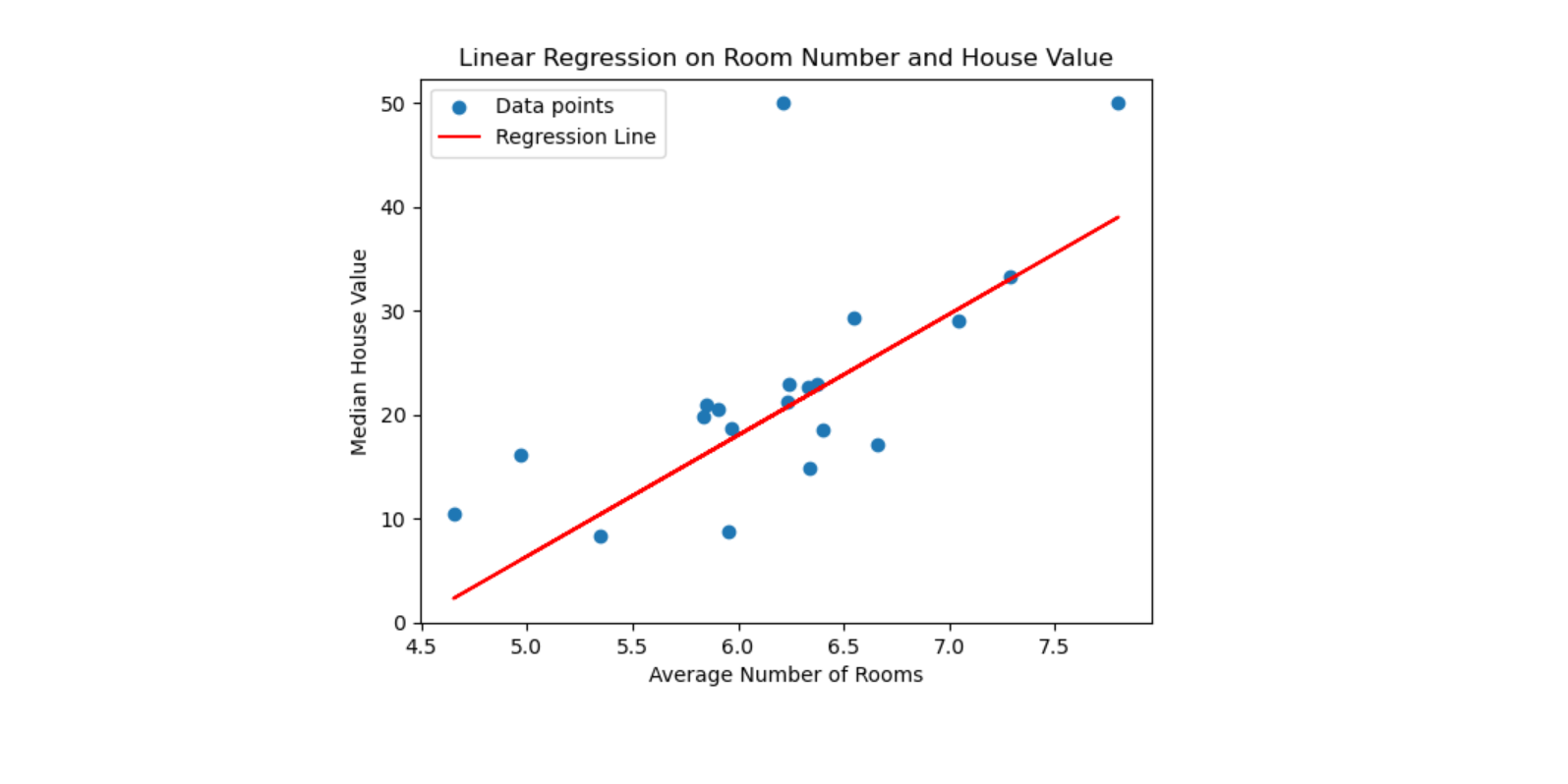
这段代码首先从UCI机器学习库加载波士顿房价数据集,然后从中随机抽取20个样本点来分析房间数量(RM)和房屋中位数价格(MEDV)之间的关系。接着,使用一个自定义的非线性模型(包括高达五次的多项式项)来拟合这些数据点,并利用均方误差(MSE)损失函数和梯度下降算法来训练模型。最后,代码绘制了一个散点图,展示了原始数据点和拟合的多项式回归线,以直观地展示模型的拟合效果。此代码旨在探索房间数量对房价的影响,并尝试使用一个复杂一些的非线性模型进行拟合。
看完李宏毅老师的课以后,发现他讲的宝可梦的例子很好,但是没有他的数据集,就按照他的讲法用其他数据集写了一下。
纯手写
可以加深理解,但是效果没有sklearn的好
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data"
col_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
data = pd.read_csv(url, sep='\s+', names=col_names)
print("数据总数", len(data))
print("前5条数据", data.head(5))
# 从数据集中随机选取20个数据点
sample_data = data.sample(20, random_state=0) # random_state=0表示每次随机抽样的结果都一样
RM = sample_data['RM']
MEDV = sample_data['MEDV']
# 定义线性回归模型
def linear_model(x, w, b):
return b + w * x # 当然这里可以定义任意的线性模型 或者 任意的非线性模型 例如:return b + w * x + w2 * x ** 2
# 定义MSE损失函数
def mse_loss(y_true, y_pred):
return np.mean((y_true - y_pred) ** 2)
# 初始化参数
w = np.random.rand()
b = np.random.rand()
# 设置学习率和迭代次数
learning_rate = 0.00001
iterations = 1000
# 梯度下降
for i in range(iterations):
# 计算当前预测值
y_pred = linear_model(RM, w, b)
# 计算梯度
w_grad = -2 * np.mean(RM * (MEDV - y_pred))
b_grad = -2 * np.mean(MEDV - y_pred)
# 更新参数
w -= learning_rate * w_grad
b -= learning_rate * b_grad
# 计算损失
loss = mse_loss(MEDV, y_pred)
if i % 100 == 0:
print(f"Iteration {i}: Loss = {loss}, w = {w}, b = {b}")
# 最终模型参数和损失
print(f"Final model: w = {w}, b = {b}, Loss = {loss}")
# 绘制房间数量与房价的关系
plt.scatter(RM, MEDV, label='Data points')
plt.xlabel('Average Number of Rooms')
plt.ylabel('Median House Value')
plt.title('Linear Regression on Room Number and House Value')
# 绘制回归直线
x = np.linspace(min(RM), max(RM), 100) # 生成一系列房间数的值
y = linear_model(x, w, b) # 使用模型计算对应的预测房价
plt.plot(x, y, color='red', label='Regression Line')
plt.legend() # 显示图例
# 显示图表
plt.show()如果使用的是非线性的函数,会产生这样的函数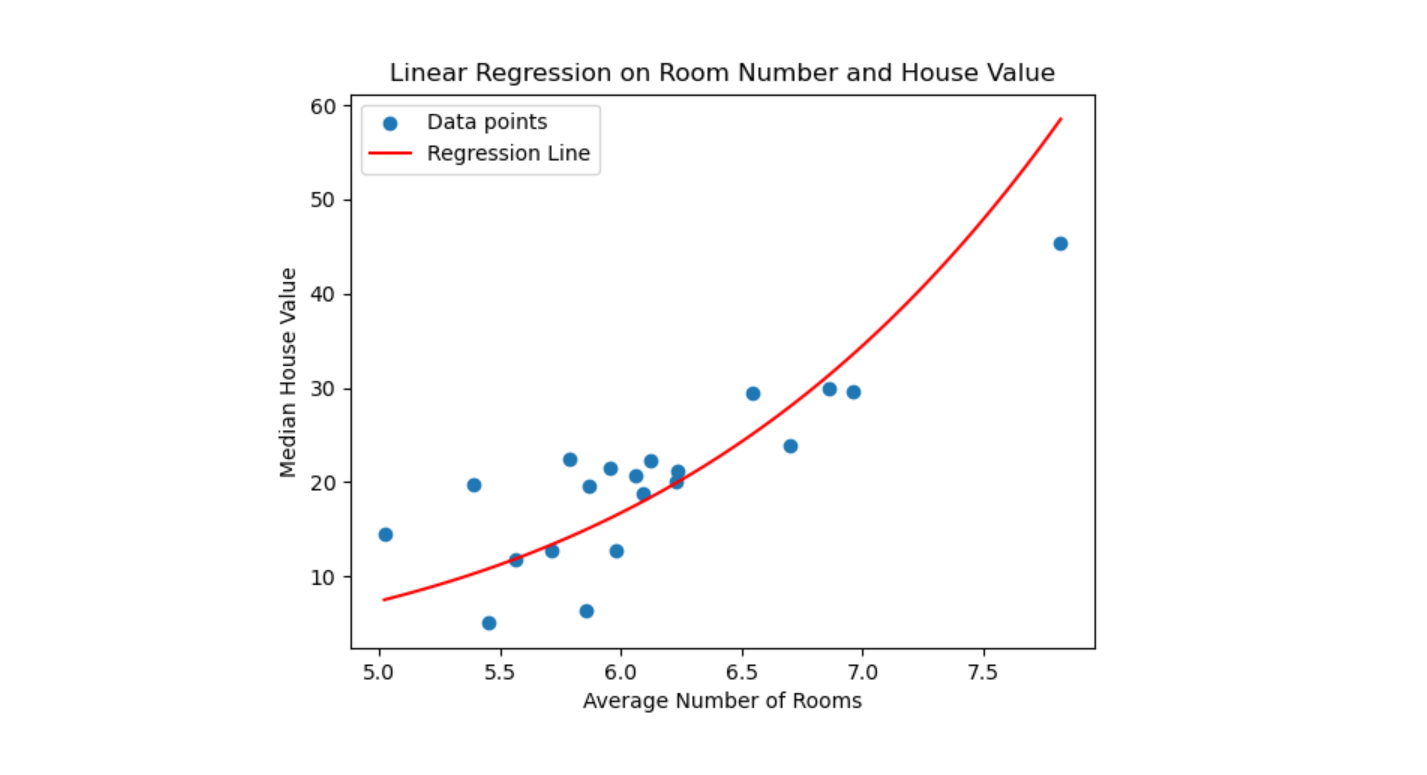
使用sklearn
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 加载数据
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data"
col_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
data = pd.read_csv(url, sep='\s+', names=col_names)
# 从数据集中随机选取20个数据点
sample_data = data.sample(20, random_state=0)
X = sample_data[['RM']] # 特征: 房间数量 返回值类型: DataFrame
y = sample_data['MEDV'] # 目标: 房价 返回值类型: Series
# 划分数据集(可选)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 计算MSE
mse = mean_squared_error(y_test, y_pred) # (均方误差,MSE)是评估回归模型性能的一种常用指标。它计算预测值与实际值之间的平均平方差异。MSE 越小,模型的预测性能越好。
print(f"Mean Squared Error: {mse}")
# 绘制房间数量与房价的关系
plt.scatter(X, y, label='Data points')
plt.plot(X, model.predict(X), color='red', label='Regression Line') # 绘制回归线
plt.xlabel('Average Number of Rooms')
plt.ylabel('Median House Value')
plt.title('Linear Regression on Room Number and House Value')
plt.legend()
plt.show()

